The xintercept of a function is calculated by substituting the value of f (x) as zero Similarly, the yintercept of a function is calculated by substituting the value of x is zero The slope of a linear function is calculated by rearranging the equation to its general form, f (x) = mx c;Where m is the slopeThe output f (x) is sometimes given an additional name y by y = f (x) The example that comes to mind is the square root function on your calculator The name of the function is \sqrt {\;\;} and we usually write the function as f (x) = \sqrt {x} On my calculator I input x for example by pressing 2 then 5 Then I invoke the function by pressing
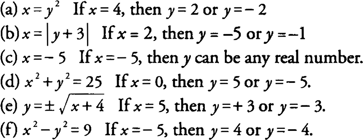
Functions
F x function equation
F x function equation-Solution First, we have f(0) = 0 Let c = f(1) Using the math induction, we have f(x 1 x n) = f(x 1) f(x n) Let x 1 = = x n = x Then we get f(nx) = nf(x) for any positive integer n Let x = 1=mwhere mis a nonzero integer Then we have f(n m) = nf(1 m) On the other hand, mf(1 m) = f(1) = c Thus we have f(n m) = nf(1 m) = c n mAn equation with infinite solutions means X = All real numbers So, you would be able to pick any number for X and the equation would be true This doesn't work for you equation If x=13, then the only value that is a valid solution is 13 If you pick another



1 1 Four Ways To Represent A Function Mathematics Libretexts
F (x)f (y)=xy f (x) −f (y) = x −y is a functional equationFree graphing calculator instantly graphs your math problemsGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
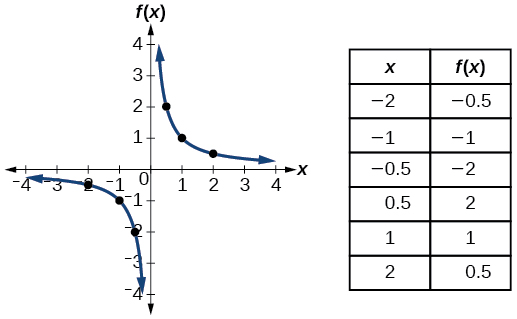
So this function f (x) = 1 x x 2 Is the same function as f (q) = 1 q q 2 h (A) = 1 A A 2 w (θ) = 1 θ θ 2 The variable (x, q, A, etc) is just there so we know where to put the values f (2) = 1We are here to assist you with your math questions You will need to get assistance from your school if you are having problems entering the answers into your online assignment Phone support is available MondayFriday, 900AM1000PM ET You may speak with a member of our customer support team by callingSuppose f is a realvalued function and c is a real numberIntuitively speaking, the expression → = means that f(x) can be made to be as close to L as desired, by making x sufficiently close to c In that case, the above equation can be read as "the limit of f of x, as x approaches c, is L" AugustinLouis Cauchy in 11, followed by Karl Weierstrass, formalized the definition of the limit
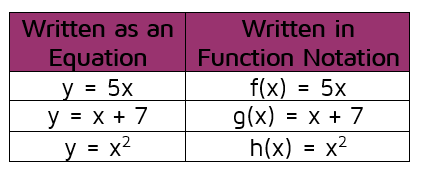
A function is an equation that has only one answer for y for every x A function assigns exactly one output to each input of a specified type It is common to name a function either f(x) or g(x) instead of y f(2) means that we should find the value of our function when x equals 2Math Quadratic equations If the roots of the quadratic equation x2 x 1 =0 be α and β then the equation whose roots are α^00 and β^00 is A x2 x 2 = 0 Bx2 x 1 = 0 Cx2 2x 1 = 0 Dx2 xWe set the denominator,which is x2, to 0 (x2=0, which is x=2) When we set the denominator of g (x) equal to 0, we get x=0 So x cannot be equal to 2 or 0 Please click on the image for a better understanding




Graphs Types Examples Functions Video Lesson Transcript Study Com



Inverse Functions
A function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular valuesFind fofnegativeone") In either notation, you do exactly the same thing you plug –1 in for x , multiply by the 2 , and then add in the 3 , simplifying to get a final value of 1Find f (–1)" (pronounced as "fofx equals 2x plus three;




Evaluating And Solving Functions College Algebra




53 Pts The Function F X 7 X 1 Is Transformed To Function G Through A Horizontal Compression By A Brainly Com
Algebra problems with detailed solutions Problem 1 Solve the equation 5( 3x 2) (x 3) = 4(4x 5) 13 DetailedA math reflection flips a graph over the yaxis, and is of the form y = f (x) Other important transformations include vertical shifts, horizontal shifts and horizontal compression functions parent functions reflection Precalculus Introduction to Functions CCSSMath 8FA1 , HSFIFA1, HSFIF that input is it will produce a given a given output so what is an example of a function so I could have something like f of f of X and X tends to be the variable most used for an input into the function and the name of a function tends to be f tends to be the most used variable but we'll see that



1
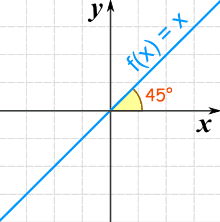



Linear Equations
It is a different way of writing "y" in equations, but it's much more useful!Now you say "f (x) = 2x 3; Section 31 The Definition of the Derivative In the first section of the Limits chapter we saw that the computation of the slope of a tangent line, the instantaneous rate of change of a function, and the instantaneous velocity of an object at \(x = a\) all required us to compute the following limit \\mathop {\lim }\limits_{x \to a} \frac{{f\left( x \right) f\left( a \right)}}{{x




What Is A Function



Equation Wikipedia
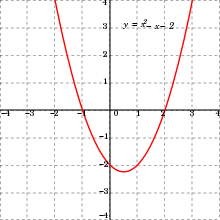
F(x) = (x 1) 2 4 From this equation, we can already tell that the vertex of the parabola is at ( 1,4 ), and the axis of symmetry is at x = 1 Now all that has to be done is to plug in points around the vertex, then graphFind x intercept(s) of the graph of an equation Evaluate functions Find the slope of a line passing through two points Find slope of a line from its equation Find equation of a line Solve equation with absolute value;Solve problems from Pre Algebra to Calculus stepbystep \square!




Quadratic Equations Functions 2 X Quadratic Equations Have




Find The Equation For The Inverse Function F 1 X Chegg Com
The maths styles can be set explicitly For instance, if you want an inline mathematical element to display as a equationlike element put \displaystyle before that element There are some more maths stylerelated commands that change the size of the text Inline maths elements can be set with a different style \ (f(x) = \displaystyle \fracStart with the equation beautiful math coming please be patient $\,y=f(x)\,$ Replace every $\,x\,$ by $\,k\,x\,$ to give the new equation $\,y=f(k\,x)\,$ This causes the $\,x$values on the graph to be DIVIDED by $\,k\,$, which moves the points closer to the $\,y$axisLearning Outcomes Evaluate and solve functions in algebraic form Evaluate functions given tabular or graphical data When we have a function in formula form, it is usually a simple matter to evaluate the function For example, the function f (x)= 5−3x2 f ( x) = 5 − 3 x 2 can be evaluated by squaring the input value, multiplying by 3, and



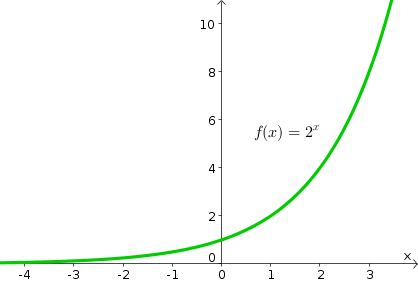
Exponential Functions Transformations And Applications Intomath




Function Operation Definition Overview Video Lesson Transcript Study Com
We dash the line if the values on the line are not included in the boundary If the values are included we draw a solid line as before Second we test a point in each region If one point on one side of the line satisfies our inequality, theConcavity (new) End Behavior (new) Average Rate of Change (new) Holes (new) Piecewise Functions Continuity (new) Discontinuity (new) Arithmetic & Composition CompositionsShort Solution Steps \frac { f ( x \Delta x ) f ( x ) } { x \Delta x } x Δ x f ( x Δ x) − f ( x) Multiply x and x to get x^ {2} Multiply x and x to get x 2 \frac {f\left (x\Delta x\right)fx} {x^ {2}\Delta } x 2 Δ f ( x Δ x) − f x Factor the expressions that are not already factored



Functions And Linear Equations Algebra 2 How To Graph Functions And Linear Equations Mathplanet




Using Transformations To Graph Functions
In this video I try to explain what a function in maths is I once asked myself, why keep writing y=f(x) and not just y!??PDE's Oliver Knill, Math 21a On this handout we deal with functions f(t,x) of two variables These functions satisfy equations containing partial derivatives called partial differential equationsThe F(x) Column Formula row in Origin worksheet lets you directly type expressions to calculate column values based on data in other columns and metadata elements The expression can be further edited in the Set Values dialog which provides a lower panel to execute Before Formula scripts for preprocessing data The Set Values dialog also provides a search button to quickly




4 Ways To Find The Range Of A Function Wikihow




How Do You Find F X If You Have A Value For X Virtual Nerd
In order to find what value (x) makes f (x) undefined, we must set the denominator equal to 0, and then solve for x f (x)=3/ (x2);F ( x) = x2 A function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around For instance, the graph for y = x2 3 looks like this This is three units higher than the basic quadratic, f (x) = x2 Basics Function f (x) Let's begin the basics by defining what a function is Based on our introduction, for something to be called by it, it must satisfy two conditions A function is a relation or a link between two sets – a collection of like things A function must follow a "onetoone" or "manytoone" type of relationship




Let F R R Be A Continuous Onto Function Satisfying F X F X 0 X In R If F 3 2 And F 5 4 In 5 5 Then The Equation F X 0 Has



Function Notation P3 Kate S Math Lessons
The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}\left (f4\right)x5=0 x2 (∣f ∣ − 4) x − 5 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, f4 for b, and 5 for c in the quadratic formula, \frac {Differential equations of the form d y d x = f (x) \frac{dy}{dx}=f(x) d x d y = f (x) are very common and easy to solve The following shows how to do it Step 1 First we multiply both sides by d x dx d x to obtain d y = f (x) d x dy=f(x)~dx d y = f (x) d x StepI've since realised that 'y' can b



The Exponential Function Math Insight
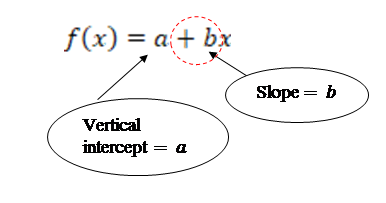



3 Slope Intercepts Graphs
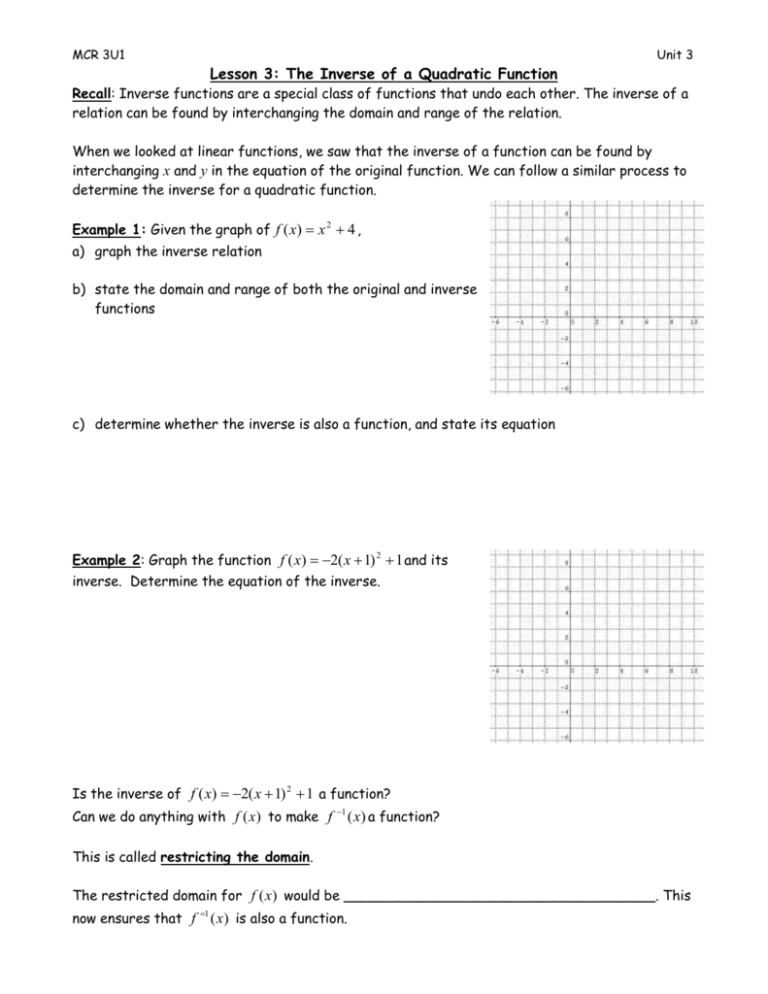
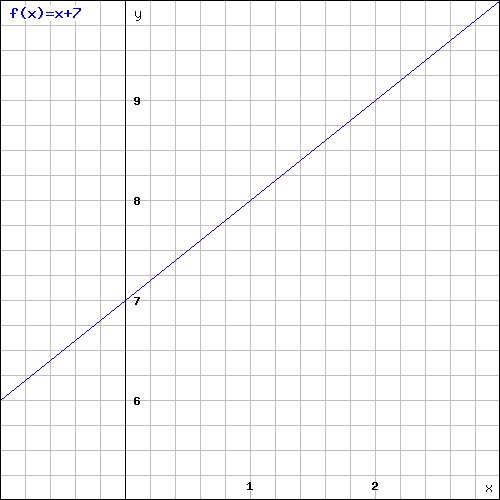
Start with the equation y =f(x) y = f ( x) Subtracting p p from the previous y y values gives the new equation y= f(x)−p y = f ( x) − p This shifts the graph DOWN p p units A point (a,b) ( a, b) on the graph of y= f(x) y = f ( x) moves to a point (a,b−p) ( a, b − p) on the graph of y= f(x)−p y = f ( xIn the original equation, replace f(x) with y to 2 Replace every x in the original equation with a y and every y in the original equation with an x Note It is much easier to find the inverse of functions that have only one x termF(x) means function of x For x any number, f(x) depends on the value of x Example If f(x) = x 2 and x = 6 then f(x) or f(6) = 62 = 8 Example If f(x) = x^2 1 and x = 5 then f(5) = 5^2 1 =25 1 = 24 In each case x is a variable input The output is f(x) which also varies depending on the x value used as input f(x) is often referred to as y
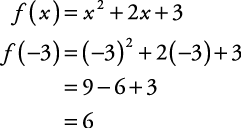



Function Notation




Quadratic Functions Equations Dev Serum
Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank youMost often you'll see functions written as f ( x) = an equation, wherein the equation can be as complex as a multivariable expression or as simple as an integer Examples of functions f ( x) = 6 f ( x) = 5 x − 12 f ( x) = x 2 2 x − 4 Functions can always be graphed and different kinds of functions will produce different looking graphs35 minutes ago Thanks for contributing an answer to Mathematics Stack Exchange!
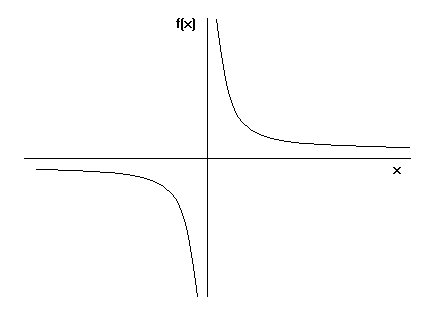



Functions Algebra Mathematics A Level Revision




Bol Com Avoid Negativity F X Ixi Math Equation Journal For Math Teacher Or Math Lover
Graph inequalities In order to graph an inequality we work in 3 steps First we graph our boundaries;Please be sure to answer the questionProvide details and share your research!Example Question #1 How To Find F (X) Possible Answers Correct answer Explanation \ (\displaystyle f (6)= 2 (6)^2 62\) \ (\displaystyle 2\times ×3662\) \
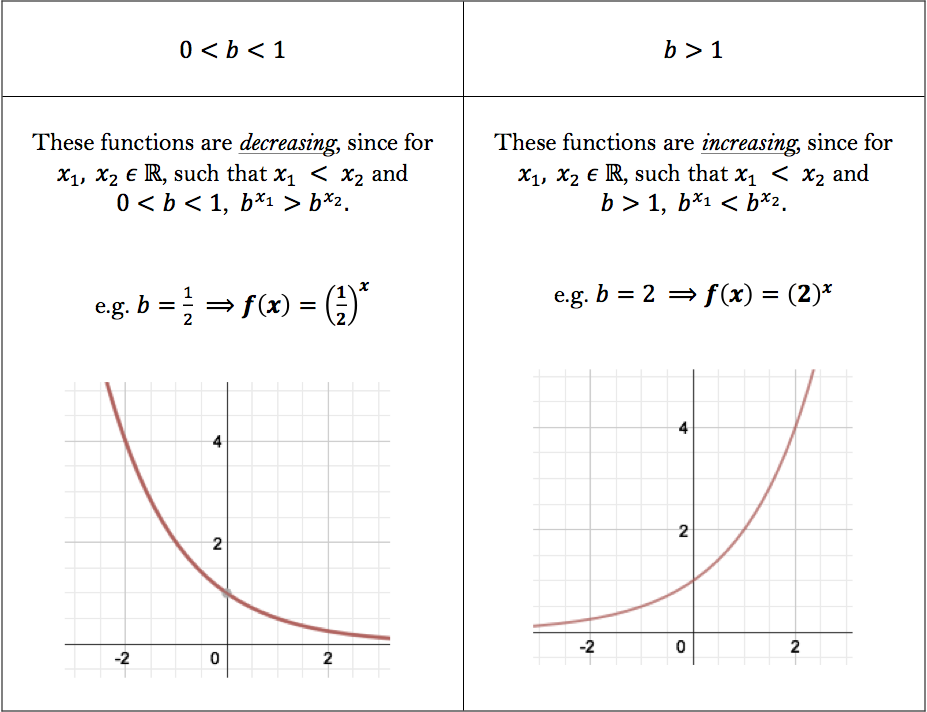



Functions And Their Inverses Worked Examples




The Various Types Of Basic Single Kernel Functions Download Table
U(a;t) = u(b;t) = 0 Then we'll consider problems with zero initial conditions but nonzero boundary values We can add these two kinds of solutions together to get solutions of general problems, where both the initial and boundary values are nonzero D DeTurck Math 241 002 12C Solving the heat equation 4/21But avoid Asking for help, clarification, or responding to other answersThe symbol f(x), which is often used to name an algebraic expression in the variable x, can also be used to denote the value of the expression for specific values of x For example, if f(x) = 2x 4 where f{x) is playing the same role as y in Equation (2) on page 285, then f(1) represents the value of the expression 2x 4 when x is




A Real Valued Function F X Satisfies The Function Equation F X Y
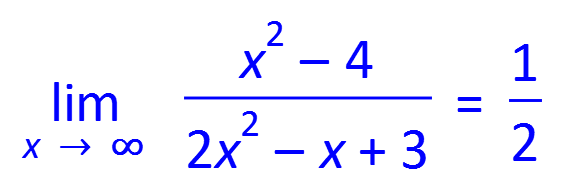



Efofex Software
f(x) = 1 x for x ∈ 1 05, 05;F(x) = 05 for x ∈ 07, ∞) On the interval 05, 07, we can choose f to be any continuous function such that f(05) = 1 05, f(07) = 05 and the values of f are all in the interval 1 05, 05



1 Polynomial Functions And Equations




Functions And Linear Equations Algebra 2 How To Graph Functions And Linear Equations Mathplanet
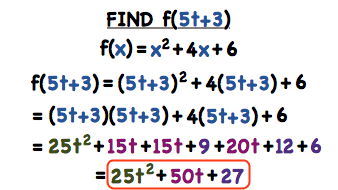



How Do You Find F X When The Value For X Contains Other Variables Virtual Nerd
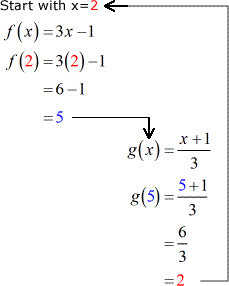



Verifying If Two Functions Are Inverses Of Each Other Chilimath




Composite Functions Youtube




3 1 Graphs Of Quadratic Functions Mathematics Libretexts
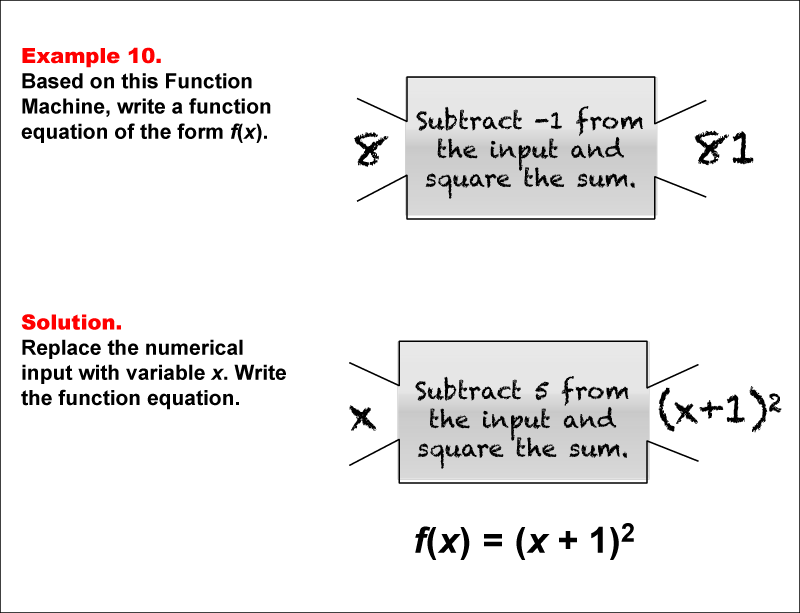



Math Example Function Rules And Equations Example 10 Media4math
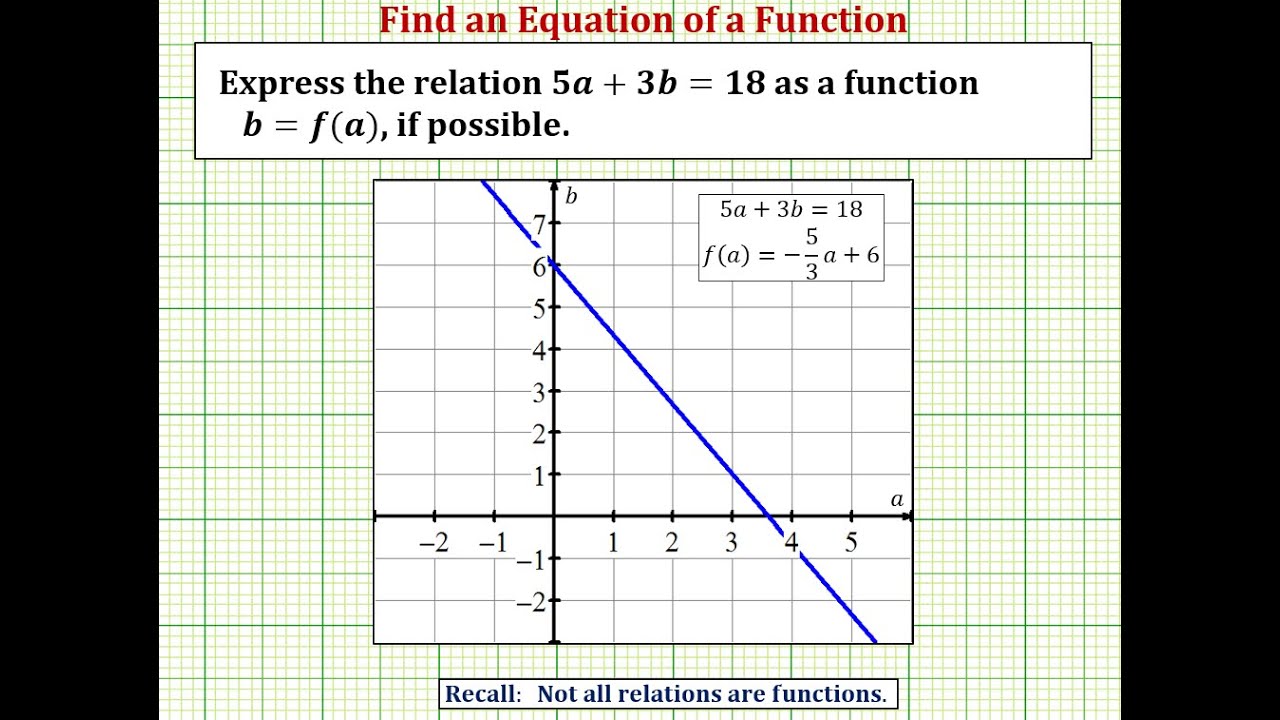



Evaluating And Solving Functions College Algebra




Exponential Function And Equations Revie Free Sat Practice




Composite Functions Video Lessons Examples And Solutions
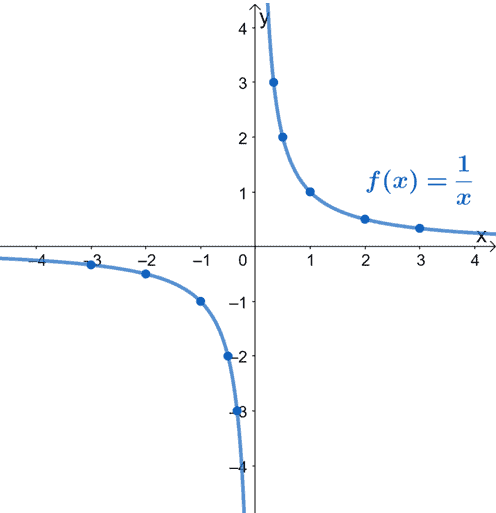



How To Graph Reciprocal Functions By Transformation




Linear Equations In Function Notation Simplifying Math Youtube




Properties Of Elementary Functions Ppt Video Online Download



1




Exponential And Logarithmic Functions And Equations Ppt Download
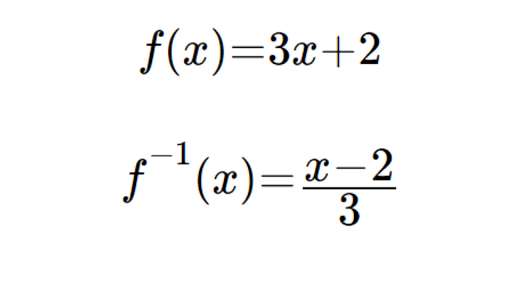



Finding Inverse Functions Article Khan Academy




3 2 Representing Functions



Quadratic Functions




4 Ways To Find The Range Of A Function Wikihow




Function Notation Writing Equations Algebra Lessons Notations




The Equation Defines A One To One Function F F X Chegg Com




Evaluating And Solving Functions College Algebra
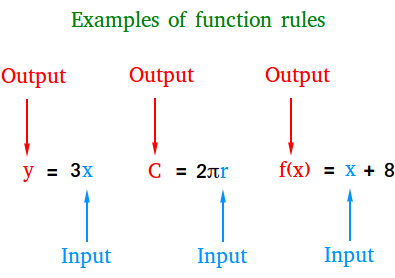



Write A Function Rule
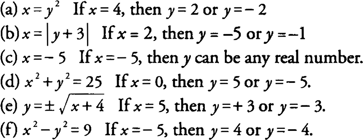



Functions




Evaluating Composite Functions Calculus Equation Solving
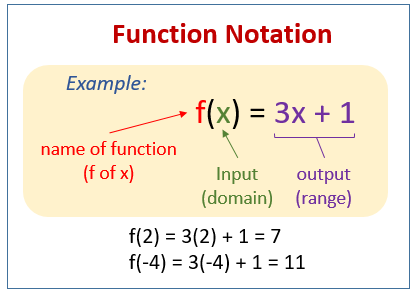



Function Notation Examples Solutions Videos
(141).jpg)



Quadratic Functions And Equations Quiz 1 Proprofs Quiz
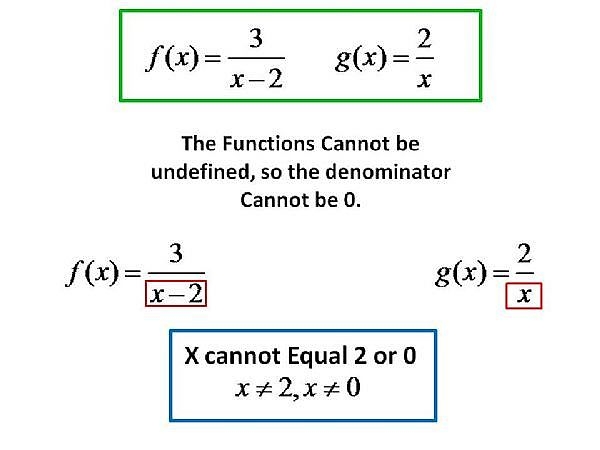



How To Determine Whether The Relation Is A Function




Piecewise Functions Justin Skycak
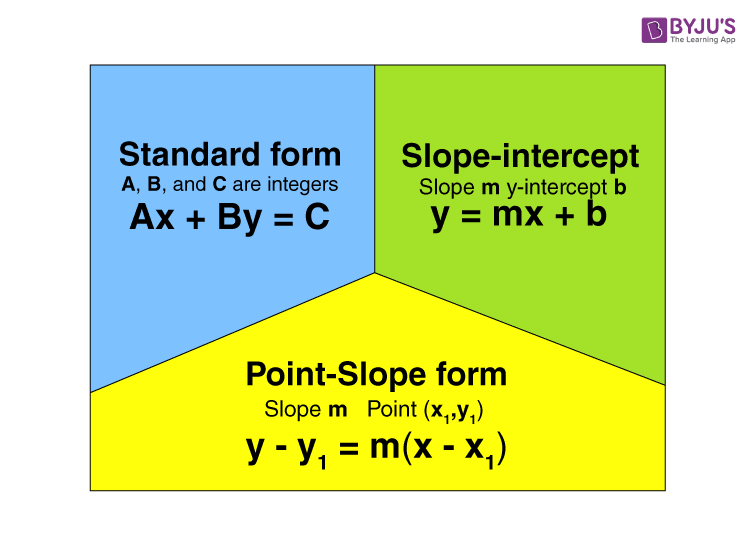



Linear Function Definition Graphs Formula Examples




Solving Functions Tables Graphs Equations Simplifying Math Youtube




How To Graph Trigonometric Functions Video Lesson Transcript Study Com




Functions And Equations




Constant Function Wikipedia




Why Is This Solution To Equation F X G X Also Possible Mathematics Stack Exchange
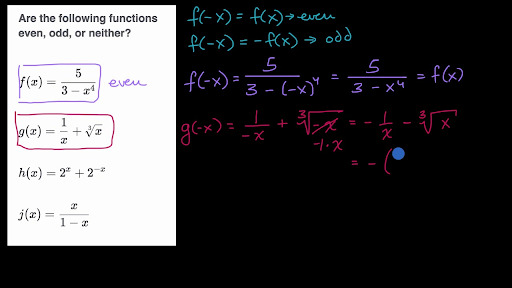



Even And Odd Functions Equations Video Khan Academy



How To Determine Whether An Equation Is A Function Or Not Quora



Math Scene Equations Iii Lesson 3 Quadratic Equations
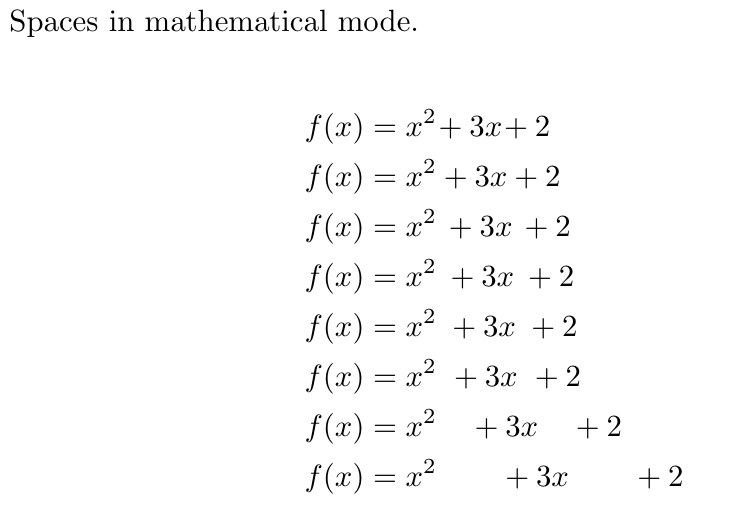



Spacing In Math Mode Overleaf Online Latex Editor



3




Logarithmic Functions Equations And Inequality Math Yahoo
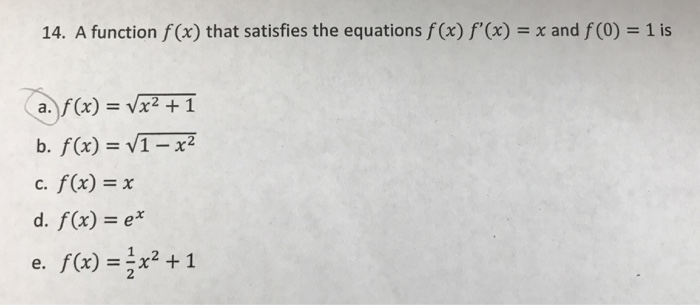



A Function F X That Satisfies The Equations F X Chegg Com



Quadratic Function Homework Help




Jaws Does Not Read The Equation Just After The Html Table In Ie Browser Stack Overflow




Derivative Of Inverse Functions How To W Examples




Example 15 Show X Y Dy Dx X 2y Is Homogeneous Solve



Untitled Document




Functions Algebra 1 Math Khan Academy




1 1 Four Ways To Represent A Function Mathematics Libretexts




Graphing Square Root Functions




Compositions Of Functions




Math Fonts In Microsoft Office Random Walks



Math Scene Equations Iii Lesson 3 Quadratic Equations




Function Notation P3 Kate S Math Lessons




Equations Of Functions Ck 12 Foundation



Geogebra Tutorial Functions




7 2 Transformations Of Exponential Functions Math 30




6 Ways To Find The Domain Of A Function Wikihow



Math Scene Equations Iii Lesson 3 Quadratic Equations




Even And Odd Functions Equations Video Khan Academy
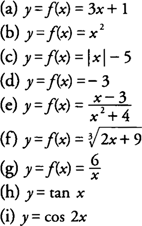



Functions



Q Tbn And9gcsmm4ktmxrxm10kmsg3wqo5rzire Ogwbm0v2tajixhbesgniod Usqp Cau
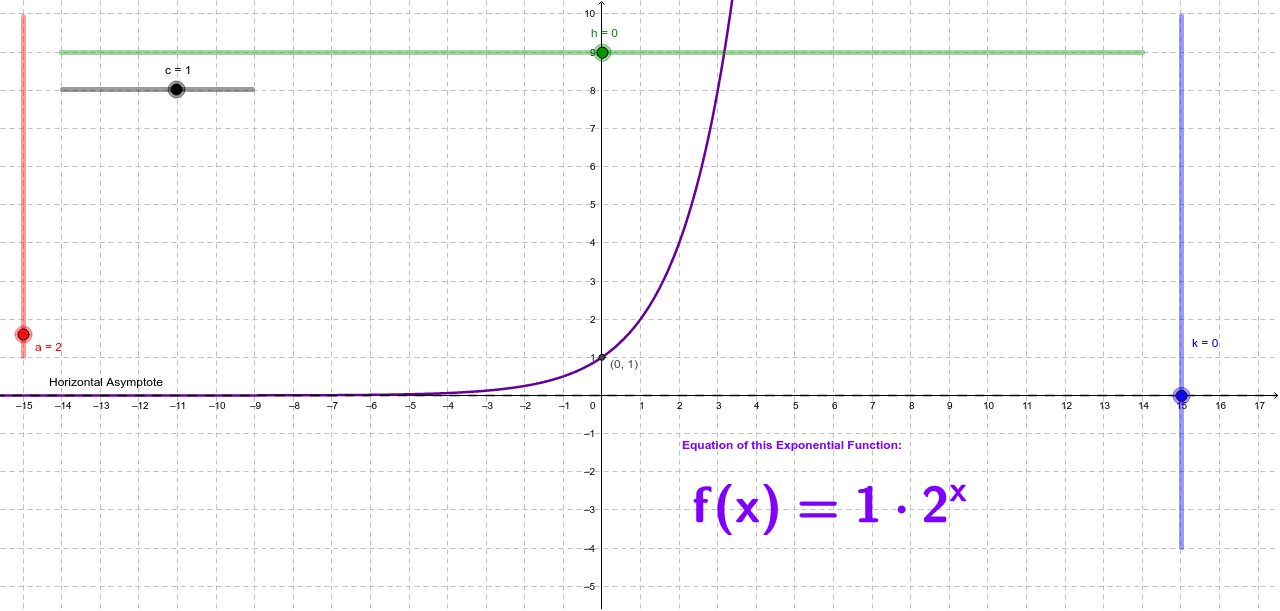



Exponential Functions Graph Equation Anatomy Geogebra



Linear Functions
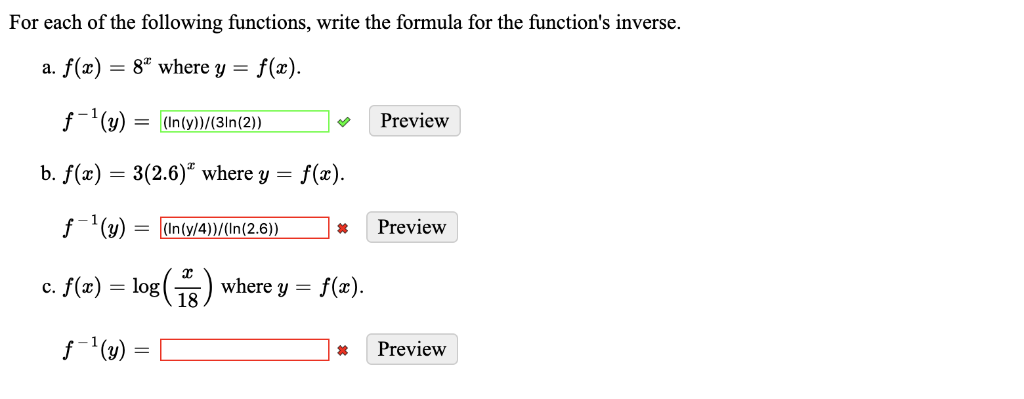



For Each Of The Following Functions Write The Chegg Com



Download Fx Equation 21 09 02
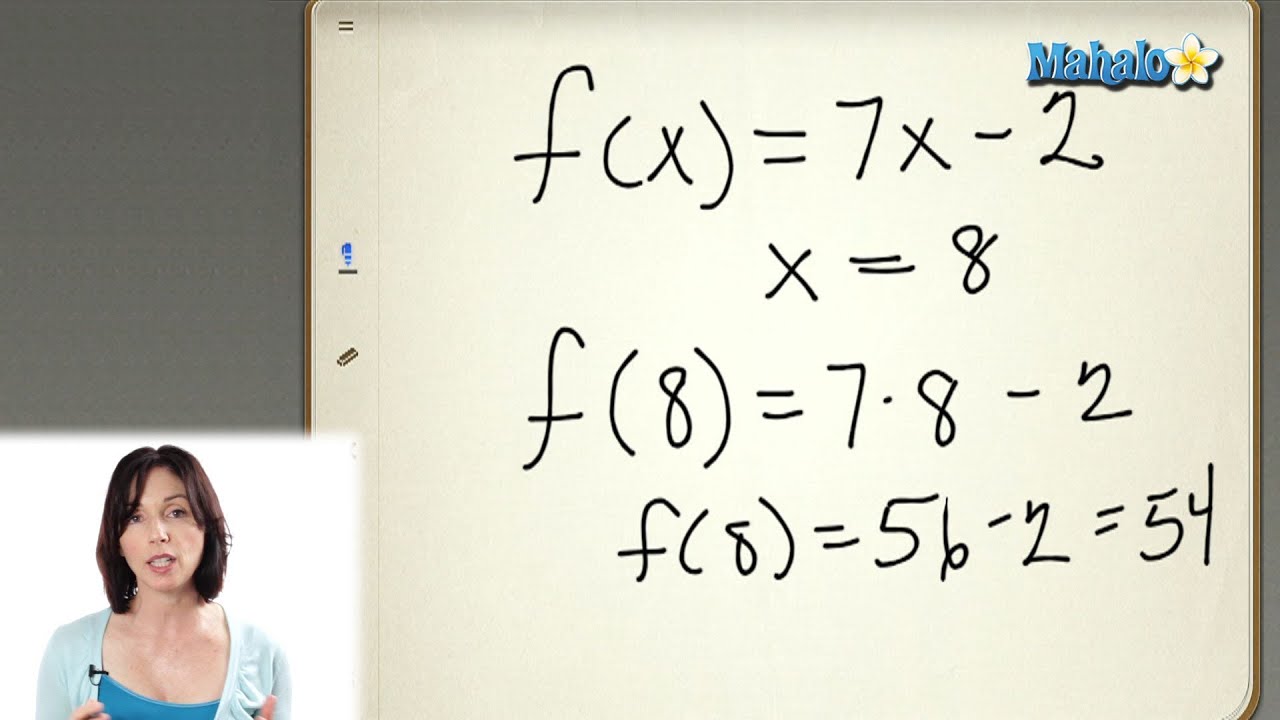



Linear Functions Youtube
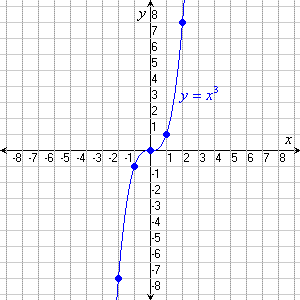



Cubic Functions



Linear Functions And Equations Slope Intercept Form Zona Land Education




Trigonometry




2 2 Functions And Relations Functions Siyavula




Using Function Notation What Is F X Youtube




Equation Of A Polynomial Function Mathematics Stack Exchange



Secant Mathematics Britannica
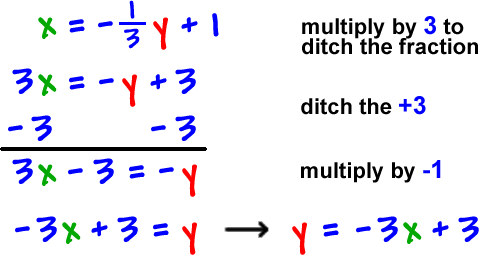



How To Find The Inverse Of A Function 1
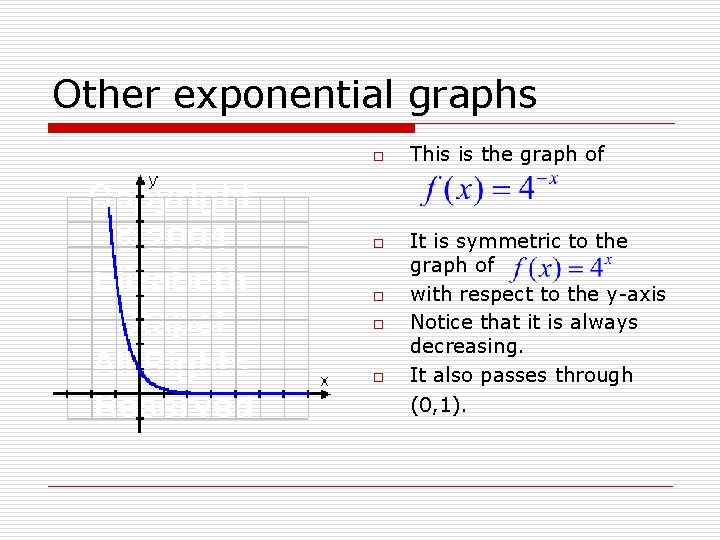



Exponential Functions The Equation Defines The Exponential Function



0 件のコメント:
コメントを投稿